Микромагнитное моделирование поведения намагниченности в инвертированных опалоподобных структурах

27.11.2017 16:04

В ноябре 2017 года младший научный сотрудник ОИКС (НИЦ «Курчатовский институт» – ПИЯФ) Дубицкий Илья Семенович завершил цикл микромагнитных расчетов, позволивших вычислить магнитный форм-фактор инвертированных опалоподобных структур (ИОПС) на основе кобальта.

Инвертированные опалы могут быть получены из коллоидных кристаллов посредством заполнения пустот между сферами каким-либо ферромагнитным материалом с последующим удалением самих сфер. В результате образуется пространственно-упорядоченная трехмерная сеть наноузлов, соединенных между собой удлиненными контактами. Сложная топология сети приводит к появлению неожиданных свойств и красивых явлений. Так в 2013 году сотрудники ПИЯФ выдвинули гипотезу о принадлежности ИОПС к классу трехмерных искусственных спиновых льдов [1]. Однако большой период трехмерной структуры ИОПС (800 nm) не позволяет непосредственно восстановить все детали ее магнитного строения даже с помощью самых современных экспериментальных методик, что затрудняет явную проверку гипотезы.

Понимание магнитных свойств инвертированных опалов может быть достигнуто только с помощью совместного применения экспериментальных техник и численного моделирования. В качестве метода моделирования была выбрана модель микромагнетизма [2]. Эта модель позволяет проводить расчеты фактически «из первых принципов», используя только хорошо известные параметры материала и геометрические характеристики изучаемой наноструктуры. Основное ограничение подхода состоит в использовании модели непрерывной среды. Тем не менее микромагнитные расчеты позволяют удивительно точно описывать магнитное поведение наносистем, размер которых превышает несколько десятков нанометров.

Микромагнитное моделирование поведения локальной намагниченности в ИОПС позволило подтвердить гипотезу спинового льда [3]. Были предсказаны значения геометрических параметров инвертированных опалов (толщины контактов), при которых следствия модели спинового льда должны проявиться наиболее ярко.

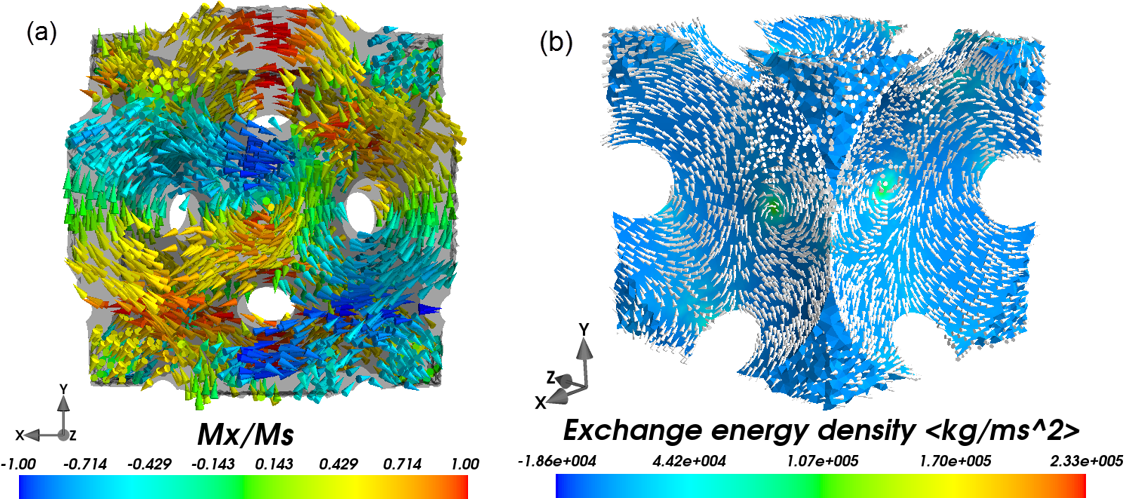
Вычисленное распределение намагниченности в элементарной ячейке ИОПС (слева) и в структурном элементе ИОПС ‑ квазикубе (справа). Размер ячейки составляет примерно 800 nm.

Вычислен магнитный форм-фактор ИОПС и его изменение во внешнем магнитном поле. Результаты моделирования находятся в согласии с данными SANS, полученными в нейтронном центре имени Хайнца Майера-Лейбница, Гархинг, Германия, на установке SANS-1.

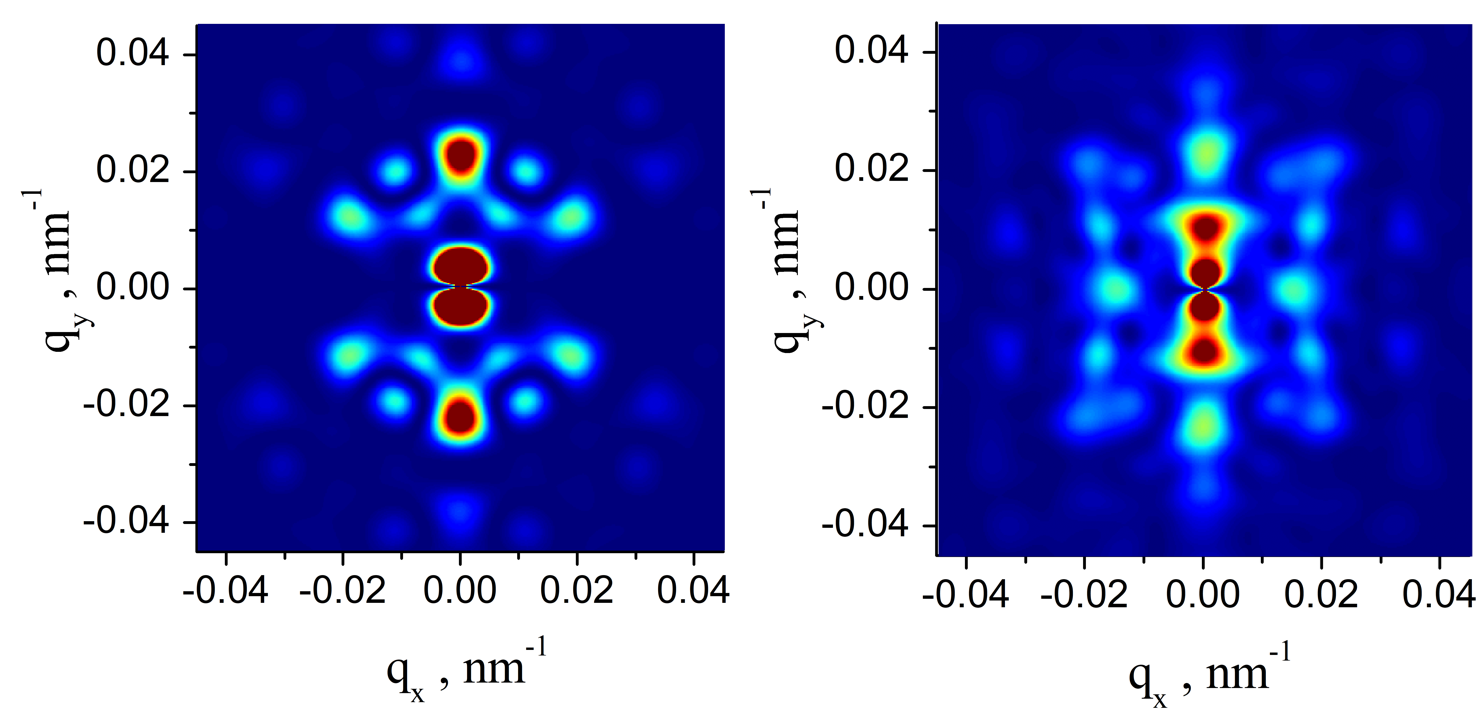Результаты вычисления картины SANS, обусловленной магнитным форм-фактором, при приложении внешнего магнитного поля вдоль направления [121] мезоструктуры ИОПС. Состояние насыщения (слева) и остаточной намагниченности (справа).

Следует отметить, что инвертированные опалы являются единственным известным в настоящий момент трехмерным искусственным спиновым льдом. Все остальные члены данного семейства наноструктур представляют собой двумерные системы.

Методика интерпретации данных малоуглового рассеяния нейтронов на магнитных наноструктурах с помощью микромагнитного моделирования, разработанная коллективом сотрудников ПИЯФ, является во многом уникальной. Ранее подобное сочетание методов использовалось только для исследования объемных ферромагнетиков [4]. В то же время не вызывает сомнений, что данная техника будет крайне высоко востребована в ближайшем будущем в связи с совершенствованием технологий синтеза и поиском трехмерных структур, обладающих качественно новыми свойствами [5].

[1] A. Mistonov, N. Grigoryeva, A. Chumakova, H. Eckerlebe, N. Sapoletova, K. Napolskii, A. Eliseev, D. Menzel, and S. Grigoriev, PRB 87, 220408 (2013).
[2] A. Aharoni, Introduction to the Theory of Ferromagnetism, Oxford University Press, New York, (2001).
[3] I. Dubitskiy, A. Syromyatnikov, N. Grigoryeva, A. Mistonov, N. Sapoletova, and S. Grigoriev, Journal of Magnetism and Magnetic Materials 441, 609 (2017).
[4] S. Erokhin, D. Berkov, N. Gorn, and A. Michels, PRB 85, 024410 (2012).
[5] A. Fernández-Pacheco, R. Streubel, O. Fruchart, R. Hertel, P. Fischer, and R. P. Cowburn, Nature Communications 8, 15756 (2017)