Кубические ФМ с взаимодействием Дзялошинского-Мория

Направления / Магнетизм и сильнокоррелированные системы / Кубические ферромагнетики с взаимодействием Дзялошинского-Мория

Кубические ферромагнетики с взаимодействием Дзялошинского-Мория

Systems with Dzjaloshinskii-Moriya interaction under applied field: Fe_1-xCo_xSi and MnSi

V. A. Dyadkin, S.V. Grigoriev, S.V.Maleyev, A.I.Okorokov, Yu.O.Chetverikov (PNPI, Gatchina, St.Petersburg, Russia)
D. Menzel (Technische Universitat Braunschweig, Braunschweig, Germany)
P.Boni, D. Lamago, R.Georgii (TU Munchen, Garching, Germany)
H.Eckerlebe (GKSS Forschungszentrum, Geesthacht, Germany)

Скачать постер: [1] Скачать публикации по теме: [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11]

Fe_1-xCo_xSi and MnSi structure

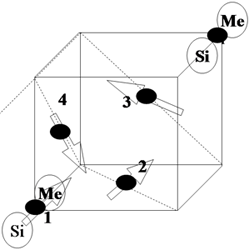
1) Space group P2₁3, a = 0.4558 nm.

2) 4 Me-atoms and 4 Si atoms
     (u,u,u), (1/2+u,1/2-u,u),
     (1/2-u,-u,1/2+u) (-u,1/2+u,1/2+u)
     with u_Me = 0.138 and u_Si = 0.845

3) with
for Fe_1-xCo_xSi where x = 0.05 –0.80.
with .

4) period of the spiral 30 - 300 nm for Fe_1-xCo_xSi
period of the spiral 18 nm for MnSi.

[1] Y. Ishikawa, K Tajima, D. Bloch and M.Roth, Soild State Commmun. 19 (1976) 525.
[2] Y. Ishikawa, G. Shirane, J.A. Tarvin, M. Kohgi, Phys.Rev.B 16 (1977) 4956.
[3] J. Beille, J. Voiron, M. Roth, Solid State Commmun. 47 (1983) 399.

Magnetic order and resistance in Fe_1-xCo_xSi and MnSi

NB!!! Magnetism and metallic properties are correlated at small x

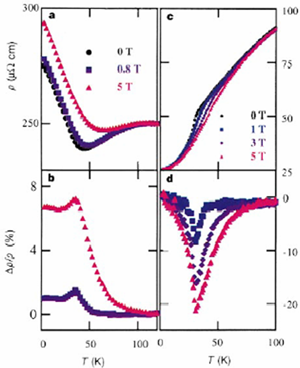
The resistivity and magnetoresistance for crystalline Fe_1-xCo_xSi and polycrystalline MnSi versus temperature.

N. Manyala, Y. Sidis, J. F. DiTusa, G. Aeppli, D.P. Young, Z. Fisk, Nature 404 (2000) 581

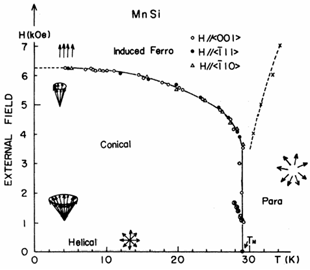
Phase diagram

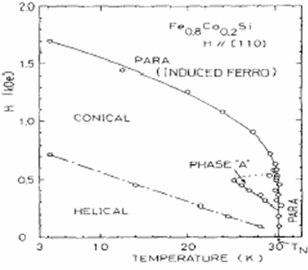
MnSi		Fe_0.8Co_0.2Si

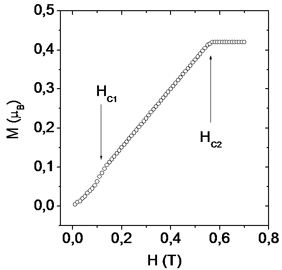[1] Y. Ishikawa, G. Shirane, J.A. Tarvin, M. Kohgi, Phys.Rev.B 16 (1977) 4956.		[2] K. Ishimoto, H. Yamaguchi, Y. Yamaguchi, J. Suzuki, M. Arai, M. Furusaka, Y. Endoh, J.Magn.Magn.Mat. 90&91 (1990) 163.

Driving forces of cubic system with DM.

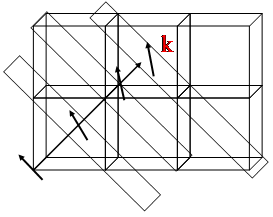
Free energy density
1) isotropic ferromagnetic exchange
W(q) = (A/2) (q² + k₀²) S_q² +

2) antisymmetric spin exchange Dzyaloshinskii-Moria (DM) due to lack of a symmetry center:
+ D (q [S_q ´ S _-q])+
handedness (left) is determined by sign and value of D.

3) weak anisotropic exchange (AE) interaction fixes direction of spiral along <1,1,1> :
+ (F/2)(q_x² |S_q^x| ² + q_y² |S_q^y| ² + q_z² |S_q^z| ² )

[1] I.E. Dzyaloshinskii, Sov. Phys. JETP 19 (1964) 960.
[2] P.Bak, M.H.Jensen, J.Phys. C13 (1980) L881.

Driving forces of cubic system with DM

k-dependent part of the classical energy [P.Bak, M.H.Jensen, J.Phys. C13 (1980) L881.]

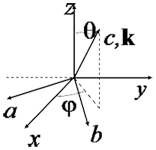Hierarchy of interactions: A >> D a >> F

For components of k:

For k:

Driving forces of cubic system with DM

Bak-Jensen model:

(i)

(ii)

(iii) if D₀ < 0 then left-handed spiral & if D₀ > 0 then right-handed spiral

(iv) Direction of k is not fixed by the Dzialoshinskii interaction. It is the anisotropic exchange

, which does !!!

Driving forces in magnetic system of MnSi

Substitute

into

Sc_i² (a_i² + b_i²) is maximal and equal to 2/3 at (k || c || [111]) and
is minimal and equal to 0 at (k || c || [100])

If F < 0, then E_cl is minimized at (k || c || [111]);
If F > 0, then E_cl is minimized at (k || c || [100]).

Interaction of the helix with the field

1) A k² = g m_B H_C2 critical field of the induced ferromagnetism
2) k = S D/ A the helix wavevector

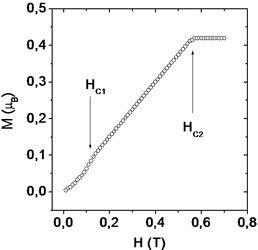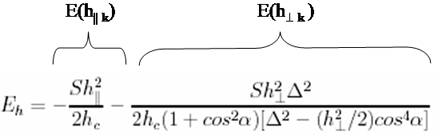
Field contribution to the GS energy

		The field dependent part of the ground state energy [S.V. Maleyev, PRB 73 (2006) 174402 ]

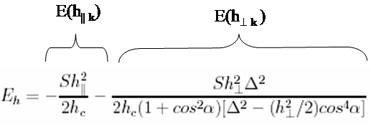		E(h_\|\|) = h_\|\|k S sin a - classical Zeeman energy E(h_{^ k} ) – quantum contribution describing the interaction of the helix structure with the field h_{^ k} .

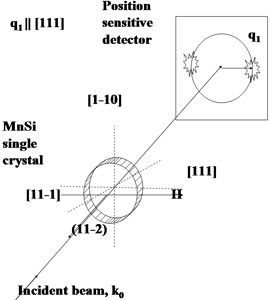
Experimental geometry

Bragg conditions:

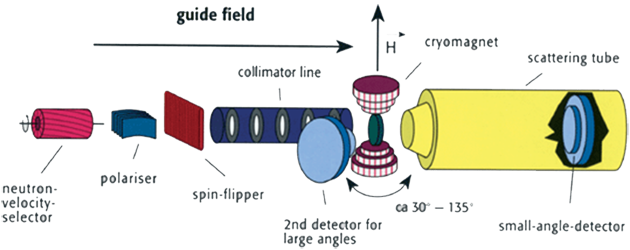
Experimental setup

The installation SANS-2 at FRG-1 in Geesthacht (Germany).

P₀=0.95, l=0.58 nm, (lD/l=0.1)

Field induced k-flop in MnSi near T_C

S.V. Grigoriev, S.V. Maleyev, A.I. Okorokov, Yu.O. Chetverikov, H. Eckerlebe, Phys.Rev.B 73 (2006) 224440.

T ~ T_C

		Four domains spiral structure
		The single domain spiral structure
		k-flop
		The single domain spiral structure again

Interpretation: orientation of the helix under applied field


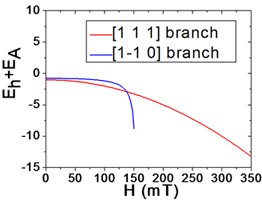
Conclusion: the existence of spin wave gap stabilizing magnetic structure with respect to the small field h_{^ k} has been experimentally proved.		(E_h + E_A)(H) for H \|\| [111]: k \|\| [111] branch and k \|\| [1-1 0] branch for parameters H_C2 = 340 mT and D = 100 mT.

Magnetic field evolution


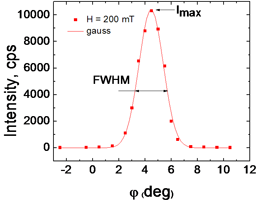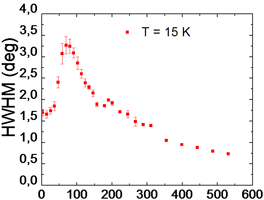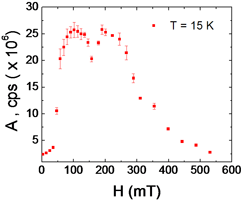Rocking scan	Magnetic mosaic	Total intensity

(H-T) Phase diagram

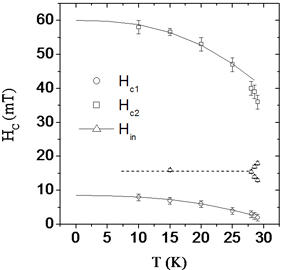
Fe_1-xCo_xSi : parameters of the system

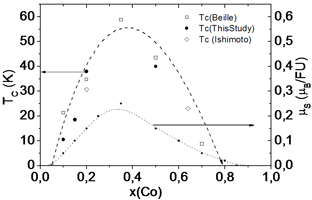
What are parameters of the system?

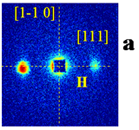
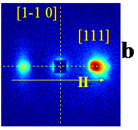
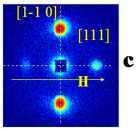
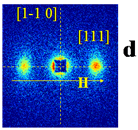
Maps of the SANS intensities for four different samples Fe_1-xCo_xSi and x = 0.10 , 0.15, 0.20, and 0.50

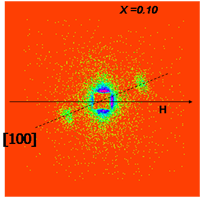
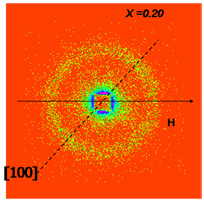
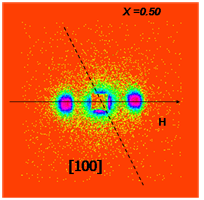
T = 9 K, H = 1 mT

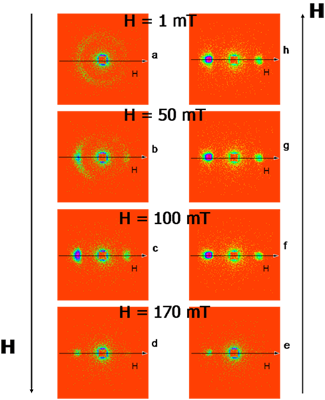
Field evolution for Fe_0.8Co_0.2Si T = 10 K

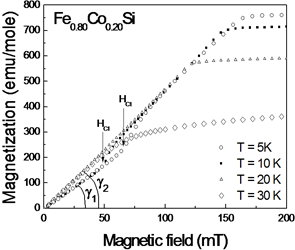
The magnetization curves taken at different temperatures T = 5, 10, 20, 30 K.

Data analysis: field evolution

The neutron intensity along the ring at q = q_C, i.e. as a function of the angle between H and q for Fe_0.8Co_0.2Si at T = 10 K.

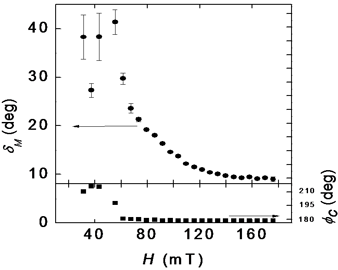
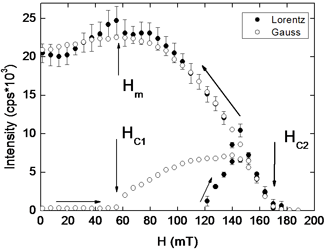
The integral neutron intensity as a function of the field at T = 10 K.

The center of Gaussian j_C and the magnetic mosaic d_M of the magnetic Bragg reflection (k || H) as a function of the magnetic field.

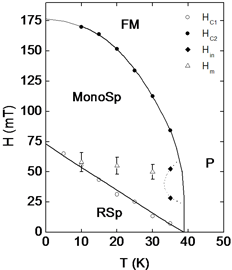
k-flop in Fe_0.8Co_0.2Si near T_C		H – T phase diagram

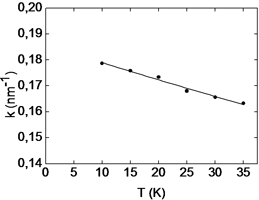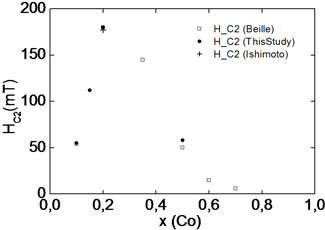
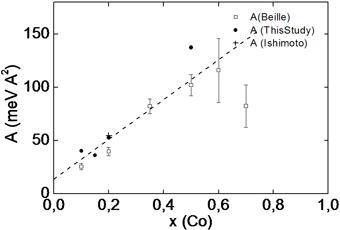
Parameters of the magnetic systemFe_1-xCo_xSi vs x

Conclusion

1. The spin wave stiffness as

was estimated. The monotonous dependence of A on the concentration x demonstrates absence of any correlation between this parameter A and the critical temperature T_C.

2. The DM interaction was also estimated. The x-dependence repeats practically the magnetic T - x phase diagram showing that either D (DM interaction) or S is responsible for the order parameter of these compounds.

3. The spin wave gap was obtained from the minimum in the field dependence of the peak intensity near T-C. It is shown that the value of the gap is .

вверх