Motivation
The chirality, in general, is attracting much attention in a wide variety of disciplines from biology to chemistry and physics. For example, one of the authors of this work is a left-handed person and the others are right-handed. Considering this fact, one can conclude that there must be an internal ”right-handed chiral” force in the bodies of human-beings pushing us to ”right” and building obstacles on the way to the ”left”. The similar phenomenon takes place in physics of the helical spin structures of the crystals with lack of the center symmetry of its crystallographic structure, which create the one-handed helix (chirality) due to internal ”chiral” force called antisymmetric Dzyaloshinskii-Moriya (DM) interaction [1, 2]. However, the right- and left-handed helices are energetically equivalent in materials, which do have a crystallographic center of inversion. In particular, such chiral degeneracy occurs in the rare-earth elements Ho and Dy, which are planar helical magnets. |
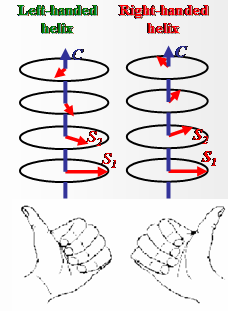 |
The polarized neutron scattering in helimagnets [6,7]
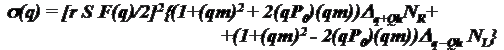
s(q) – neutron cross section
q - momentum transfer
NR,NL- the populations of the left and right-handed chiral domains
Qh- the helix scattering vector
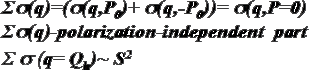
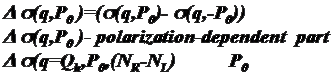
A sample- Y50nm[Dy4.3nm/Y2.8nm]350/Y234nm/ Nb200nm Al2O3 is a superlattice similar to that used in [8,9], which grown by molecular-beam-epitaxy techniques in the plane perpendicular to the [001] c-axis of the hexagonal Dy and Y structure as a single crystal. Below TN = 166 K, a coherent spin helix whose characteristic coherence length is much longer than the thickness of the Dy/Y double layer appears, whereas the bulk Dy ferromagnetic transition at TC = 89 K is suppressed [8,9]. |
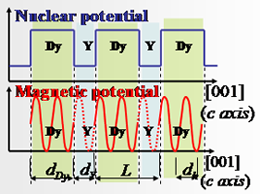 |
The coherent spin helix penetrates through paramagnetic Y layers due to the charge density wave of conduction electrons. dh = 2.3nm – Helix period |
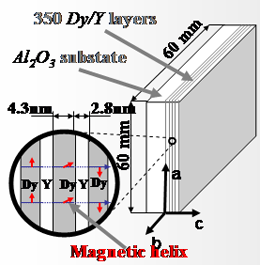 |
Experimental detales
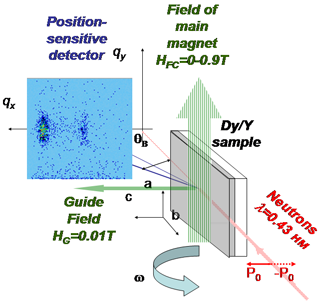
The experiments were carried out at the NeRo reflectometer of FRG-1 research reactor in Geesthacht (Germany).
The scattered neutrons were detected by the position sensitive detector (PSD) with (256x256) pixels. Bragg condition 2dsinQB/2=l with q = 2/d was satisfied for several peaks associated with the interaction of neutrons with the spin helix and nuclear superstructure.
The polarization followed the direction of the guide magnetic field of order of 0.01T, which was applied perpendicularly to the incident beam and perpendicularly to multilayer surface (along c-axis).
The main magnetic field HFC from 0.01 to 0.9T could be applied, when necessary, perpendicularly to the incident beam and parallel to multilayer surface.
|
 |
|
The scattering intensity was measured in the temperature range from T=100 to T=200 K for two incident polarizations I(±P0) along and opposite to the guide magnetic field. |
||
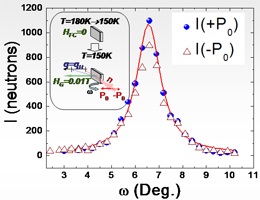
q scan
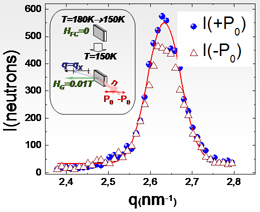
The magnetic Bragg peak is observed below TN = 166.0 K and its intensity increases with decreasing temperature. The q-dependence of the intensity for two polarizations I(±P0) taken at w = wc is shown. It has a Gaussian distribution of the intensity centered at |q|H = 2.63 nm-1 with the width Dq = 0.09 nm-1. The coherent length of the helix domain was extracted from the width. It is of order of 2p/Dq = 70 nm. |
 |
Interpretation of polarization-dependent scattering
For our experiment (P0 || ĉ) the scattering intensity with a certain polarization is attributed to one of two types of the helix domains: left- or right- handed ones. The non-zero difference between two intensities I(+P0) and I(-P0) demonstrates existence of the non zero average chirality in the sample i.e. there is a non equal population of the left- and right- handed helixes. This difference is significant near the maximum of the peak intensity of order of 10% in Fig.1 (a and b). The difference is also noticeable in a value of a width of these curves. The more populated domains have smaller width (for 2-3 %) both in q- and w-dependence. This means that more populated domains better ordered than other ones. For comparison of two contributions to scattering coming from left- and right- handed helix domains we introduce the ratio
where I(+P0) and I(-P0) are q-integrated intensities at w = wC.
Dependence of temperature/field prehistory
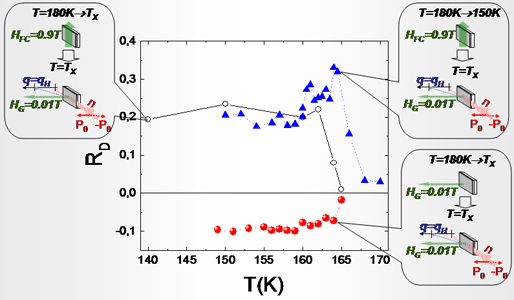
For Zero Field Cooling (ZFC – red symbols) RD is negative and decreases from zero at T above TN to (–0.1) at low temperature. Fitting of RD to the scaling function of t=(TN – T)/TN gives the value bC-2b=0.22 in a good agreement with the previous experiment on SANS2 [5]. It should be noticed that thermocycling (cooling up and down through the critical temperature range in zero field) has no effect on the value of RD.
The sample, being cooled to a certain T in the field H=0.9T applied in the sample plane (H ^ĉ) and measured in a small guide field (H || P0 || ĉ), gives RD value of the opposite sign than in the ZFC experiment. Now RD is zero above TN and positive (+0.2) below TN (open symbols).
Even more intriguing behavior of RD is observed for measurements after FC (H=0.9T) to 150 K with the subsequent warming up in zero field (blue symbols). RD is constant in the range from 150 to 160 K, and then increases as temperature approaches TN. It has maximum at TN, and then decreases to zero in the paramagnetic range.
Magnetic control of chirality
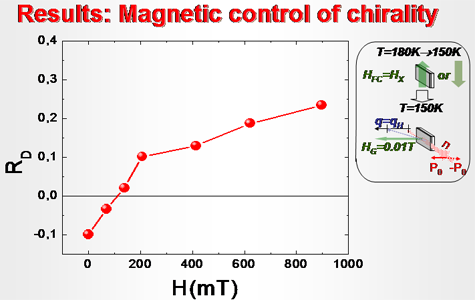
The value RD depends on the strength of the magnetic field applied in the sample plane in the FC procedure but it does not depend on the direction (±) of the field. It is clear that the magnetic field applied upon cooling is able to change RD and repopulate the left- and right-handed domain structure.
Conclusions
We have observed the spin chirality, or, the non-equal helix domain population numbers in the Y/Dy multiplayer system upon zero field cooling below TN. Furthermore the field-induced chirality have found after cooling in the magnetic field applied in the (ab) plane of the sample. This break the chiral degeneracy is mostly forming in the critical temperature range near TN.
References
[1] I.E. Dzyaloshinskii, Zh. Exp. Teor. Fiz. 46, 1420 (1964)[Sov.Phys. JETP 19, 960 (1964)].
[2] P.Bak, M.Jensen, J.Phys. C 13, L881 (1980).
[3] V.P.Plakhty, W.Schweika, Th. Bruckel, J. Kulda, S.V.
Gavrilov, L.-P.Regnault, D. Visser, Phys.Rev.B 64 (2001) 100402(R).
[4] K. Siratory, ... J.Phys.Soc.Jpn. 48 (1980) 1111.
[5] S. V. Grigoriev, A. I. Okorokov, Yu. O. Chetverikov,… JETP Letters 83 (2006) 478.
[6] S.V.Maleyev, V.G. Bar’jakhtar, R.A. Suris, Fiz.Tv.Tela 4 (1962) 3461
[7] M. Blume, Phys.Rev. 130 (1963) 1670.
[8] M.B.Salamon, S. Sinha, … Phys.Rev.Lett. 56 (1986) 259.
[9] RossW. Erwin, J.J. Rhyne, M.B.Salamon,… Phys.Rev.B 35 (1987) 6808.