Spin wave dynamics of Fe65Ni35 invar studied by polarized SANS
S.V. Grigoriev, A.I. Okorokov, S.V. Metelev (Petersburg Nuclear Physics Institute, St.Petersburg, Russia)
H. Eckerlebe (GKSS Forschungszentrum, Geesthacht, Germany)
N.H. van Dijk (Interfacultair Reactor Instituut, TUDelft, JB Delft, The Netherlands)
The goal is: to examine the behaviour of spin-wave stiffness of FeNi invar in the range of low q and w in the wide temperature range.
The method is: θ and w antisymmetric small-angle scattering of polarized neutrons in the ”inclined geometry” experiment.
Basic result is: in contrast to the conventional low-temperature dependence of spin-wave stiffness D(T)=D0(1-AT5/2) it was found that the whole ferromagnetic phase of Fe65Ni35 is critical and D is described as D=D0τx, where τ=(Тс-Т)/Тс, with the critical exponent х=0.48±0,01 for the range 0.1<τ< 0.9. It indicates that invar FeNi alloys are close to the quantum critical point.
In compliance with Bloch the temperature dependence of the saturation magnetization Ms is Ms (T)=Ms(0)(1-BT3/2), where В=[2.612qμH/ Ms(0)]( kB/4πD)3/2), kВ is the Boltzman constant and D is the spin wave (SW) stiffness, which is D(T)=D(0)(1-AT5/2) for a Heisenberg ferromagnet. There is discrepansy between SW stiffness Dm(T) as determined by calculation through the bulk magnetization and by neutron scattering Dn(T). Both of these D coincide for the majority of isotropic ferromagnetic materials apart from invar alloys. For Invars the Dm(T) decreases faster with increasing temperature than Dn(T). An extensive discussion on this problem have been done [1,2] and an idea of “hidden excitation” was proposed for the explanation of this discrepancy.
In principle this discrepancy in the values of Dm(T) and Dn(T) could be related with the fact that magnetization is measured at q=0, while the SW-stiffness is mainly counted from the value of q~kθ>>q0, where q0 is the dipolar momentum, and at q<<q0 the spin waves are suppressed by
d-d interaction. To check this hypotesis one has to measure Dn(T) at q<<q0.
Recently the "forbidden" mode of the excitations was observed at the invar composition of FeNi system [3,4]. The authors concluded that it arises from a dynamic modulation of the magnetic moments associated with the comprehensive strain in the phonon excitations. The origin of this mode is not understood yet.
Method of experiment
For determination of Dn(T) we use the method of “inclined geometry” which allows one to extract the antisymmetric polarization dependent part of the scattering:
where ε is spin–wave energy, e=q/q, m=H/Н and Гq is SW damping. As Ka(q,w) is an odd function of w for w<<T, the integral is equal to zero at usual used situation when e|| or ^m on account of angle factor (em)2:
The integral is not equal to zero only if φ ≠ 0 or π/2 and it reaches a maximum at φ=45º. This situation when angle φ between H and q is not zero or 90º was named [5-8] as “inclined geometry”. Moreover, the integral in (dσ/dΩ)a is antisymmetrical with respect to the scattering angle component θx in the k-H plane (Fig.1). This makes it possible to determine the antisymmetrical contribution as
The example of the ΔI(θ) distribution on detector plane is shown on Fig.2.
Scheme of SAPNS experiment
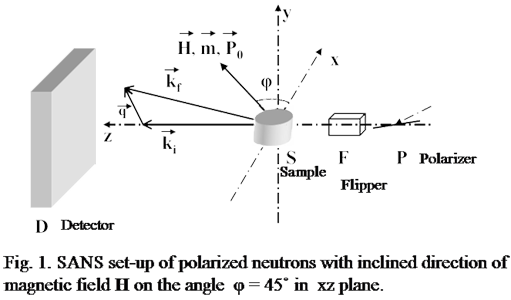
This is example of SW scattering ΔI in amorphous alloy Fe50Ni22Cr10P18[9]. θ0=mm/mn=ћ2/(2mnD) where mm is the
magnon mass and mn is neutron one.
|
 |
The study was performed on the invar sample Fe65Ni35 shaped as a plate with a width of 12 mm, length of 40 mm and a thickness of 1 mm. The alloy was prepared from pure components and homogeneized 100 h. at 1100º C. After fast cooling the sample was annealed 100 h. at 600º C.
The SAPNS experiment was performed at the SANS-2 facility of the FRG-1 reactor in Geesthacht, Germany.
Parameters of the beam: initial polarization of P0=0.95, a wavelength of λ=5.8 Å, (Δλ/λ=0.1) and divergence of 1.0 mrad. The position sensitive detector with 128x128 pixels was used. The scattering was measured in the temperature range Т=50-500 К at external magnetic field H from 1 mТ to 230 mТ applied at an angle of φ=45º with respect to the x-axis.
The experimental data are shown in Fig.3 and Fig.4.
The experimental data for invar Fe65Ni35
 |
 |
|
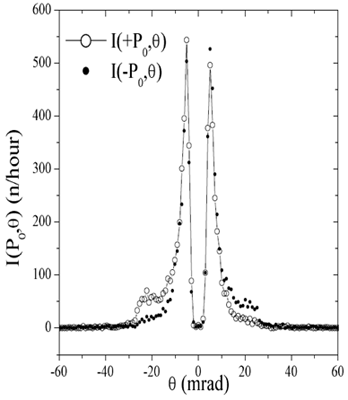
Fig.3 The form of the scattered intensity for two polarizations. On the wings one can see inflows of spin wave scattering. Minimum of intensity near θ~0 reflects the location of the beam-stop. |
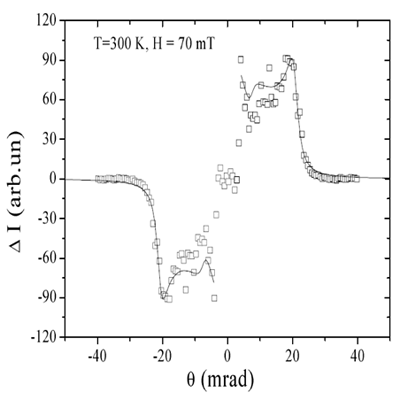
Fig.4 The result of extraction of antisymmetrical scattering |
D(T)-result
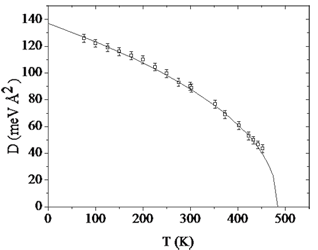
It was obtained that temperature dependence of SW stiffness D (T) for Fe65Ni35 strongly differs from law D(T)=D(0)(1-AT5/2) and is well described by the scaling relation D=D0τx, where τ=(Тс-Т)/Тс and х=0,48±0,01 in diapason 0.1 < τ <0.9 (Fig.5). The value of D0 was found D0=137±3 meVÅ2 for the w range 0,01 – 0,1meV in good agreement with the 3-axis spectrometer data for w>0,5 meV [1,2]. The TC is found to be equal to 485 К [10].
The obtained result indicates that, firstly, Dn (T=0)does not depend on diapason q, secondly, the scaling behaviour Dn(T) signifies that whole ferromagnetic phase of Fe65Ni35 is critical one. |
 |
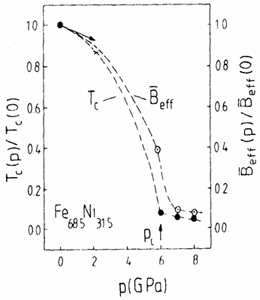
Note, that the value of TC for invar FexNi(1-x) changes drastically with increase of the external pressure from Тс≈500К at х=0.65 and at ambient pressure to Тс=0 at P≈70 kbar. The fact of dramatical change of TC was experimentally observed [11-13] (Fig.6). It means that invar Fe-Ni alloys are close to the quantum critical point (QCP). The origin of instability of the magnetic structure is unclear. One of the hypothesis for it is the presence of the small gap in the SW spectrum, which is suppressed by applied pressure. |
 |
The problem of SW gap Δ
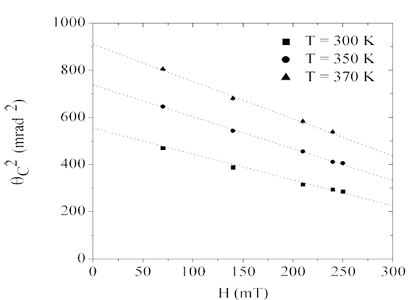
Usually the SW gap Δ is determined by extrapolation the experimentally measured dependence ε=Dq2+Δ to q →0 from the range of large q. Such extrapolation is not correct and one has to measure dispersion law at very small q. Theoretically[14] the cut-off angle θс depends on the magnetic field H and the neutron energy E as θс2(H, E)=θ02-(gμH+Δ)θ0/E, where θ0 is cut-off angle at H=0 and Δ=0. Our experiment gives linear dependence of
θс2(H) (Fig.7) for all measured temperatures and θ0 obtained from these data is constant for different H.
This result means that Δ <<gµH and it needs to perform the measurements more accurately with very high statistic and at small magnetic field H. It should be noted that method of “inclined geometry” is the unique way for estimate of the value of the gap Δ at low frequency part of spin wave spectrum. |
 |
|
Fig.7. H - dependence of θс2 |
Reference
2. S. Onodera, Y. Ishikawa, K. Tajima. J.Phys.Soc.Jap. 50 (5) (1981) 1513.
3. P.J. Brown, I.K. Jassim, K.U. Newmann, K.R.A. Ziebeck. Physica B 161 (1989) 9.
4. P.J. Brown, B. Roessli, J.G. Smith at.al, J.Phys.: Condens. Matter 8 (1996) 1527.
5. A.V.Lazuta, S.V.Maleyev, B.P.Toperverg. Sov.Phys.JETP 54 (1981) 782.
6. A.I. Okorokov, V.V. Runov, B.P. Toperverg et.al. JETP Lett. 43 (1986) 503.
7. B.P.Toperverg, V.V. Deriglazov, V.T.Mikhailova. Physica B 183 (1993) 326.
8. S.V. Grigoriev, S.V. Maleyev, A.I.Okorokov et al. Appl. Phys. A 74 (2002) 719.
9. V. Deriglazov, A.I. Okorokov, V.V. Runov, B.P. Toperverg et.al. Physica B 181-182 (1992) 262.
10. S.V.Grigoriev, S.V.Maleev, A.I.Okorokov, H.Eckerlebe, and N.H. van Dijk. Critical scattering of polarized neutrons in the invar Fe65Ni35 alloy. Phys.Rev. B 69, 134417 (2004).
11. S.V. Maleev. Zh.Eksp.Teor.Fiz. 28 (1965) 1448.
12. M.M. Abd-Elmegud and H.Micklitz. Physica B 161 (1989) 17-21.
13. M. Matsushita, S. Endo, K. Miura, F. Ono, J.M.M.M., 256 (2003) 352.
14. M. Matsushita, Y. Miyoshi, S. Endo, F. Ono, Phys.Rev.B, 72 (2005) 214404.